Чему равен угол между высотами параллелограмма? Это зависит от того, из вершины какого угла — острого или тупого — проведены эти высоты.
Утверждение I
Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма.

Дано: ABCD — параллелограмм,
∠ABC — тупой,
BM, BN — высоты параллелограмма.
Доказать:
∠MBN=∠C.
Доказательство:
1-й способ
1) Рассмотрим треугольник NBC — прямоугольный (∠BNC=90º, поскольку BN — высота параллелограмма).
Так как сумма острых углов прямоугольного треугольника равна 90º, то ∠NBC+∠C=90º.
Следовательно, ∠NBC=90º-∠C.
2) Так как BM — высота параллелограмма, то ∠MBC=90º.
∠MBC=∠MBN+∠NBC.
Отсюда, ∠MBN=90º-∠NBC.
Так как ∠NBC=90º-∠C,
∠MBN=90º-(90º-∠C)=90º-90º+∠C=∠C.
Что и требовалось доказать.
2-й способ
1)∠C+∠D=180° (как сумма односторонних углов при AD||BC и секущей CD).
Значит, ∠C=180°-∠D.
2) Сумма углов четырёхугольника равна 360°.
В четырёхугольнике MBND ∠BMD+∠BND=90°+90°=180°.
Следовательно, ∠MBN+∠D=360°-180°=180°.
Отсюда ∠MBN=180°-∠D=∠C.
Что и требовалось доказать.
Утверждение II
Угол между высотами параллелограмма, проведенными из вершины острого угла, равен тупому углу параллелограмма.
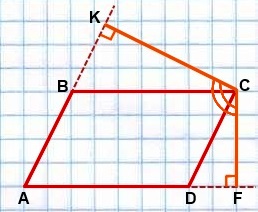
Дано: ABCD — параллелограмм,
∠BCD — острый,
CK и CF — высоты параллелограмма.
Доказать:
∠KCF=∠ABC
Доказательство:
1-й способ
1) ∠ABC+∠KBC=180º (как смежные).
Следовательно, ∠KBC=180º-∠ABC.
2) Так как CF — высота параллелограмма ABCD, то она перпендикулярна к прямым, содержащим стороны AD и BC.
Поэтому ∠BCF=90º.
3) Рассмотрим треугольник KBC — прямоугольный (∠KBC=90º, так как CK- высота параллелограмма ABCD).
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠KCB=90º-∠KBC=90º-(180º-∠ABC)=90º-180º+∠ABC=∠ABC-90º.
4) ∠KCF=∠KCB+∠BCF=∠ABC-90º+90º=∠ABC.
Что и требовалось доказать.
2-й способ
1) ∠ADC для треугольника DCF — внешний. Следовательно, он равен сумме двух внутренних углов, не смежных с ним:
∠ADC=∠DFC+∠DCF=90º+∠DCF.
2) ∠KCF=∠KCD+∠DCF.
∠KCD=90º (так как KC — высота параллелограмма). Отсюда,
∠KCF=90º+∠DCF=∠ADC.
Что и требовалось доказать.
3-й способ
1)∠A+∠ABC=180° (как сумма внутренних односторонних углов при AD∥BC и секущей AB).
Значит, ∠ABC=180°-∠A.
2) В четырёхугольнике AKCF ∠A+∠AKC+∠KCF+∠AFC=360°.
∠AKC=∠AFC=90°.
Поэтому ∠A+∠KCF=180°,
∠KCF=180°-∠A=∠ABC.
Что и требовалось доказать.
