Рассмотрим два свойства диагоналей параллелограмма.
Теорема.
I свойство диагоналей параллелограмма
Диагонали параллелограмма точкой пересечения делятся пополам.
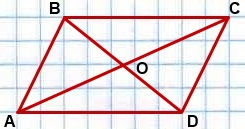 Дано:
Дано:
ABCD — параллелограмм,
AC ∩ BD=O.
Доказать:
AO=CO, BO=DO.
Доказательство:
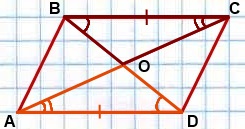
Рассмотрим треугольники AOD и COB
(важно правильно назвать треугольники!)
1) ∠ADO=∠CBO (как внутренние накрест лежащие при AD ∥ BC и секущей BD)
2) ∠DAO=∠BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC)
3) AD=BC (как противолежащие стороны параллелограмма)
Следовательно, ∆AOD= ∆COB (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон:
AO=CO, BO=DO.
Что и требовалось доказать.
II свойство диагоналей параллелограмма
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Для параллелограмма ABCD:
AC²+BD²=2(AB²+AD²).
Это свойство является следствием из теоремы косинусов. Его доказательство рассмотрим позже.
