Площадь трапеции по диагоналям и |

Как найти площадь трапеции по известным диагоналям и средней линии?

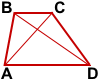ploshchad-trapecii-po-diagonalyam-i Дано: ABCD, AD∥BC,

MN — средняя линия трапеции,

AC=d₁, BD=d₂, MN=m.

Найти: S_ABCD.

Решение:

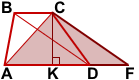ploshchad-trapecii-po-diagonalyam-i-srednej-linii 1) Проведём через вершину C прямую, параллельную диагонали BD. На пересечении этой прямой с прямой, содержащей основание AD, отметим точку F.

Имеем: CF∥BD (по построению),

BC∥DF(так как лежат на основаниях трапеции), следовательно, четырёхугольник BCFD — параллелограмм (по определению).

По свойствам параллелограмма, CF=BD=d₂, DF=BC.

2) AF=AD+DF=AD+BC.

По свойству средней линии трапеции,

$MN = \frac{{AD + BC}}{2},$

следовательно, AF=2MN=2m.

Проведём CK⊥AF.

Рассмотрим треугольник ACF.

$S_{\Delta ACF} = \frac{1}{2}AF \cdot CK = \frac{{AD + BC}}{2} \cdot CK = S_{ABCD} .$

Таким образом, задача сводится к нахождению площади треугольника ACF.

В треугольнике ACF известны все стороны: AC=d₁, CF=d₂, AF=2m.

Остаётся найти площадь треугольника по формуле Герона.

$S = \sqrt {p(p - a)(p - b)(p - c)} ,$

$p = \frac{{a + b + c}}{2},$

$p = \frac{{d_1 + d_2 + 2m}}{2},$

$S = \sqrt {\frac{{d_1 + d_2 + 2m}}{2} \cdot \frac{{d_2 - d_1 + 2m}}{2} \cdot \frac{{d_1 - d_2 + 2m}}{2} \cdot \frac{{d_1 + d_2 - 2m}}{2}}$

$S = \frac{1}{4}\sqrt {((d_1 + d_2 )^2 - 4m^2 )(4m^2 - (d_1 - d_2 )^2 )} .$

Разумеется, запоминать эту формулу не нужно. Для нахождения площади трапеции через среднюю линию и диагонали достаточно провести аналогичные рассуждения.

Задача.

Найти площадь трапеции, диагонали которой равны 15 и 13, а средняя линия равна 7.

Решение:

Проводя аналогичные приведённым выше рассуждения, находим полупериметр и площадь треугольника ACF, площадь которого равна искомой площади трапеции:

$p = \frac{{d_1 + d_2 + 2m}}{2} = \frac{{15 + 13 + 2 \cdot 7}}{2} = 21,$

$S = \sqrt {21(21 - 15)(21 - 13)(21 - 14)} = \sqrt {21 \cdot 6 \cdot 8 \cdot 7} =$

$= \sqrt {3 \cdot 7 \cdot 2 \cdot 3 \cdot 2 \cdot 4 \cdot 7} = 3 \cdot 7 \cdot 2 \cdot 2 = 84.$

Ответ: 84.

Площадь трапеции по диагоналям и средней линии

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики