Периметр ромба |

Как найти периметр ромба, зная его сторону? Как найти периметр ромба по диагоналям? Как, если известен периметр ромба, найти его сторону?

Периметр ромба равен сумме длин всех его сторон.

perimetr romba

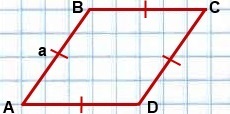
Поскольку все стороны ромба равны, то формула периметра ромба

$\underline {P = 4a} ,$

где a — длина стороны ромба.

Примеры.

1) Найти периметр ромба со стороной 7 см.

Решение:

По формуле P=4a имеем: P=4∙7=28 (см).

Ответ: 28 см.

2) Периметр ромба равен 36 см. Найти его сторону.

Решение:

По формуле P=4a имеем:

$4a = 36$

$\underline {a = 9}$

Значит, сторона ромба равна 9 (см).

Ответ: 9 см.

3) Найти периметр ромба, если его диагонали равны 12 см и 16 см.

Решение:

Чтобы найти периметр ромба, нужно знать его сторону.

${a = \frac{1}{2}\sqrt {d_1^2 + d_2^2} }$

Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям:

$P = 4a = 4 \cdot \frac{1}{2}\sqrt {d_1^2 + d_2^2}$

$\underline {P = 2\sqrt {d_1^2 + d_2^2} }$

Значит, периметр ромба с диагоналями 12 см и 16 см равен

$P = 2\sqrt {{{12}^2} + {{16}^2}} = 2\sqrt {144 + 256} =$

$= 2\sqrt {400} = 2 \cdot 20 = 40(cm).$

Ответ: 40 см.

Одна из формул для нахождения площади ромба S связывает радиус r вписанной в ромб окружности и его полупериметр p:

$S = p \cdot r$

Выразим p через S и r:

$p = \frac{S}{r}$

Так как P=2p, то приходим к формуле для нахождения периметра ромба через его площадь и радиус вписанной окружности

$2p = \frac{{2S}}{r}$

$\underline {P = \frac{{2S}}{r}}$

Периметр ромба