Медиана, проведенная к гипотенузе

Определим и докажем, чему равна медиана прямоугольного треугольника, проведенная к гипотенузе.

Утверждение.

Медиана, проведенная к гипотенузе, равна половине гипотенузы.

Доказательство:

I способ.

Дано: ∆ABC, ∠BCA=90º

Доказать: медиана, проведенная к гипотенузе, равна половине гипотенузы.

Доказательство:

1) В прямоугольном треугольнике АВС из вершины прямого угла С проведем к гипотенузе AB отрезок CO так, чтобы CO=OA.

2) ∆ AOC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

 

 

 

Значит, у него углы при основании равны:∠OAC=∠OCA=α.

 

 

 

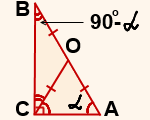
3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в треугольнике ABC ∠B=90º- α.

4) Так как ∠BCA=90º (по условию), то ∠BCO=90º- ∠OCA=90º-α.

 

5) Рассмотрим треугольник BOC.

∠BCO=90º-α, ∠B=90º- α, следовательно, ∠BCO=∠B.

Значит, треугольник BOC — равнобедренный с основанием BC (по признаку равнобедренного треугольника).

Отсюда BO=CO.

6) Так как CO=OA (по построению) и BO=CO (по доказанному), то CO=OA=BO, AB=OA+BO=2∙OA=2∙CO.

Таким образом, точка O — середина гипотенузы AB, отрезок CO соединяет вершину треугольника с серединой противолежащей стороны, значит, CO — медиана, проведенная к гипотенузе, и она равна половине гипотенузы:

   

Что и требовалось доказать.

Этот способ может быть использован для доказательства свойства медианы прямоугольного треугольника в 7 классе, поскольку опирается только на материал, уже знакомый  к моменту изучения данной темы.

Еще один способ доказательства свойства медианы, проведенной к гипотенузе, рассмотрим в следующий раз.