Вписанные многоугольники |

Любой правильный многоугольник является вписанным в окружность. Найдём, какой радиус описанной окружности имеют вписанные правильные многоугольники в общем случае и в некоторых частных случаях.

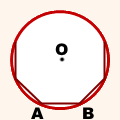opisannyj-pravilnyj-mnogougolnik Пусть дан произвольный правильный многоугольник со стороной a. Обозначим одну из его сторон AB, AB=a. O — центр описанной окружности.

opisannye-pravilnye-mnogougolniki Проведём радиусы OA и OB.Так как OA=OB, треугольник AOB — равнобедренный с основанием AB. Если многоугольник имеет n сторон и n углов (n-угольник), то его центральный угол

$\angle AOB = \frac{{{{360}^o}}}{n}.$

Проведём высоту OF. По свойству равнобедренного треугольника, OF является также его биссектрисой и медианой. Поэтому

$AF = \frac{1}{2}AB = \frac{a}{2},$

$\angle AOF = \frac{1}{2}\angle AOB = \frac{{{{180}^o}}}{n}.$

Рассмотрим прямоугольный треугольник AOF. По определению синуса,

$\sin \angle AOF = \frac{{AF}}{{AO}},$

$AO = \frac{{AF}}{{\sin \angle AOF}} = \frac{{\frac{a}{2}}}{{\sin \frac{{{{180}^o}}}{n}}} = \frac{a}{{2\sin \frac{{{{180}^o}}}{n}}}.$

Таким образом, формула радиуса описанной около правильного многоугольника окружности —

$R = \frac{a}{{2\sin \frac{{{{180}^o}}}{n}}},$

где n — количество сторон и количество углов, a — сторона n-угольника.

radius-opisannoj-okruzhnosti-pravilnogo-treugolnika В частности, при n=3 формула для нахождения радиуса описанной около правильного треугольника окружности —