Найти сторону треугольника через медиану и стороны |

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Задача

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

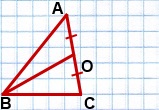
Nayti storonu treugolnika cherez medianu i storonyi

Дано: ∆ ABC,

AB=8 см,

BC=6 см,

BO — медиана, BO=√46 см.

Найти: AC.

Решение:

Nayti storonu treugolnika cherez medianu i dve storonyi

1) На луче BO отложим отрезок OD,

OD=BO.

storona treugolnika cherez medianu i storonyi

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

$A{C^2} + B{D^2} = 2(A{B^2} + B{C^2})$

$BD = 2BO = 2\sqrt {46} cm$

$A{C^2} + {(2\sqrt {46} )^2} = 2({8^2} + {6^2})$

$A{C^2} + 184 = 200$

$A{C^2} = 16$

$AC = 4cm$

Ответ: 4 см.

formula storonyi treugolnika cherez medianu i storonyi

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

${(2{m_b})^2} + {b^2} = 2({a^2} + {c^2})$

$4m_b^2 = 2({a^2} + {c^2}) - {b^2}$

$m_b^2 = \frac{{2{a^2} + 2{c^2} - {b^2}}}{4}$

${{m_b} = \frac{{\sqrt {2{a^2} + 2{c^2} - {b^2}} }}{2}}$

Найти сторону треугольника через медиану и стороны