Диагональ трапеции перпендикулярна стороне и биссектриса

Если диагональ равнобедренной трапеции перпендикулярна ее боковой стороне и диагональ — биссектриса угла трапеции, то что можно сказать о свойствах такой трапеции?

Если диагональ трапеции является биссектрисой ее угла, то боковая сторона трапеции равна одному из оснований трапеции.

Когда диагональ трапеции перпендикулярна боковой стороне, делить пополам тупой угол она не может (если один угол прямой, то и второй должен быть прямым, что невозможно).

Если диагональ равнобедренной трапеции перпендикулярна боковой стороне и делит острый угол трапеции пополам, то

1) диагональ разбивает трапецию на два треугольника: один — равнобедренный, другой — прямоугольный;

2) углы трапеции равны 60º и 120º;

3) большее основание трапеции в два раза больше меньшего основания и её боковых сторон;

4) высота трапеции равна половине её диагонали.

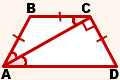
Дано: ABCD- трапеция,

AD ∥ BC, AB=CD,

   

AC — биссектриса ∠BAD.

Доказать:

1) Треугольник ABC — равнобедренный, треугольник ACD — прямоугольный;

2) ∠BAC=60º, ∠ABC=120º;

3) AD=2BC, AD=2CD;

4) высота трапеции равна половине AC.

Доказательство:

1) Поскольку

   

то треугольник ACD — прямоугольный.

∠BAC=∠DAC (так как AC — биссектриса ∠BAD по условию).

∠BCA=∠DAC (как внутренние накрест лежащие при AD ∥ BC и секущей AC).

Отсюда, ∠BAC=∠BCA.

Следовательно, треугольник ABC — равнобедренный с основанием AC (по признаку)

и AB=BF.

2) Пусть ∠BAC=∠DAC=∠BCA=xº.

∠BAD+∠BCD=180º (как противолежащие углы равнобедренной трапеции).

Следовательно, ∠BAC+∠DAC+∠BCA+∠ACD=180º.

Составляем уравнение:x+x+x+90=180, откуда x=30.

Таким образом, ∠BAC=∠DAC=∠BCA=30º, ∠BAD=∠BAC+∠DAC=60º.

∠BAD+∠ABC=180º (как внутренние односторонние при AD ∥ BC и секущей AB), откуда

∠ABC=120º.

3) В прямоугольном треугольнике ACD CD — катет, лежащий напротив угла в 30 градусов, следовательно,

   

AD=2CD, а так как CD=BC, то AD=2BC.

4) Опустим из вершины C высоту CF,

   

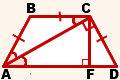В прямоугольном треугольнике ACF CF — катет, лежащий напротив угла в 30º. Поэтому

   

Что и требовалось доказать.