Рассмотрим, каким образом может быть найдена биссектриса треугольника по рисунку на клетчатой бумаге.
Задача
На клетчатой бумаге с размером клетки 1×1 изображен треугольник ABC.
Найдите длину его биссектрисы, проведённой из вершины B.
Решение:
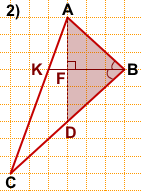
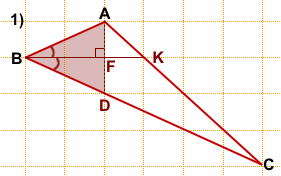 1) Треугольник ABD — равнобедренный с основанием AD.
1) Треугольник ABD — равнобедренный с основанием AD.
Отрезок BF, перпендикулярный основанию AD — высота, медиана и биссектриса треугольника ABD (по свойству равнобедренного треугольника).
Таким образом, ∠ABF=∠DBF.
Продолжим BF до пересечения со стороной AC. На пересечении BF и AC отметим точку K.
BK — биссектриса треугольника ABC, проведённая из вершины B.
Длину BK считаем по клеточкам. BF=3.
2) Треугольник ABD — равнобедренный с основанием AD.
AF — его высота, медиана и биссектриса.
Продлеваем AF до пересечения со стороной AC в точке K.
BK — искомая биссектриса треугольника ABC.
Длину BK находим по клеточкам: BK=4.
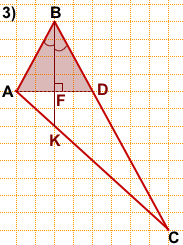 3) В равнобедренном треугольнике ABD
3) В равнобедренном треугольнике ABD
AF — высота, медиана и биссектриса.
Продолжим BF. На пересечении со стороной AC получим точку K.
BK — биссектриса треугольника ABC, длину которой нам нужно найти.
По клеточкам BK=6.
