Теорема (свойство биссектрисы равнобедренного треугольника)
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
 Дано:
Дано:
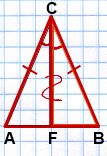
∆ ABC,
AC=BC,
CF — биссектриса.
Доказать: CF — медиана и высота.
Доказательство:
Рассмотрим треугольники ACF и BCF (важно правильно их назвать!)
1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))
2) ∠ACF=∠BCF (так как CF — биссектриса по условию).
3) сторона CF — общая.
Значит, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон и углов.
Таким образом, AF=BF, следовательно, CF — медиана.
∠AFC=∠BFC. А так как эти углы — смежные, значит, они оба прямые: ∠AFC=∠BFC=90º.
Значит, CF — высота.
Что и требовалось доказать.
