Угол, лежащий напротив диагонали ромба |

Если известны угол, лежащий напротив диагонали ромба, и эта диагональ, то, используя свойства ромба, можно найти остальные его элементы.

1) Большая диагональ ромба равна D. Напротив неё лежит угол β.

ugol-lezhashchij-naprotiv-diagonali-romba Большая диагональ AC=D, лежащий напротив неё угол ∠ABC=β (угол ромба, лежащий против большей диагонали — тупой).

Проведём вторую диагональ ромба BD, BD ∩ AC=O.

ugol-lezhashchij-protiv-diagonali-romba По свойствам ромба, его диагонали взаимно перпендикулярны, являются биссектрисами углов ромба и в точке пересечения делятся пополам. Следовательно, в прямоугольном треугольнике ABO

∠ABO=β/2, AO=D/2. По определению синуса,

$\sin \angle ABO = \frac{{AO}}{{AB}}, \Rightarrow AB = \frac{{AO}}{{\sin \angle ABO}},$

$AB = \frac{{\frac{D}{2}}}{{\sin \frac{\beta }{2}}} = \frac{D}{{2\sin \frac{\beta }{2}}}.$

Зная сторону ромба, можем найти его периметр:

${P_{ABCD}} = 4AB,{P_{ABCD}} = \frac{{4D}}{{2\sin \frac{\beta }{2}}} = \frac{{2D}}{{\sin \frac{\beta }{2}}}.$

По определению котангенса,

$ctg\angle ABO = \frac{{BO}}{{AO}}, \Rightarrow BO = AO \cdot ctg\angle ABO,$

$BO = \frac{D}{2}ctg\frac{\beta }{2}, \Rightarrow BD = 2 \cdot \frac{D}{2}ctg\frac{\beta }{2} = D \cdot ctg\frac{\beta }{2}.$

Площадь ромба может быть найдена как половина произведения его диагоналей:

${S_{ABCD}} = \frac{1}{2} \cdot AC \cdot BD, \Rightarrow$

${S_{ABCD}} = \frac{1}{2} \cdot D \cdot D \cdot ctg\frac{\beta }{2} = \frac{1}{2} \cdot {D^2}ctg\frac{\beta }{2}.$

Другой вариант — произведение квадрата стороны на синус угла:

${S_{ABCD}} = A{B^2} \cdot \sin \angle ABC,$

${S_{ABCD}} = {(\frac{D}{{2\sin \frac{\beta }{2}}})^2} \cdot \sin \beta .$

(Упростив эту формулу, получим предыдущую).

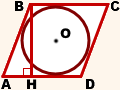po-bolshemu-uglu-romba-i-diagonali-najti Высоту ромба можно найти несколькими способами. Например, через площадь. С одной стороны, площадь ромба

${S_{ABCD}} = A{B^2} \cdot \sin \angle ABC,$

с другой —

${S_{ABCD}} = AD \cdot BH.$

Приравняв правые части формул:

$AD \cdot BH = A{B^2} \cdot \sin \angle ABC$

и разделив обе части равенства на AB (AD=AB), получим

$BH = AB \cdot \sin \angle ABC.$

(Можно найти BH непосредственно из прямоугольного треугольника ABH по определению синуса, ∠BAH=180º-β, sin∠BAH=sin(180º-β)=sinβ).

$BH = \frac{{D \cdot \sin \beta }}{{2\sin \frac{\beta }{2}}} = \frac{{D \cdot 2\sin \frac{\beta }{2}\cos \frac{\beta }{2}}}{{2\sin \frac{\beta }{2}}} = D\cos \frac{\beta }{2}.$

Радиус вписанной окружности равен половине высоты ромба

$r = \frac{1}{2}h,r = \frac{1}{2} \cdot D\cos \frac{\beta }{2} = \frac{D}{2}\cos \frac{\beta }{2}.$

2) Меньшая диагональ ромба равна d. Напротив неё лежит угол α.

ugol-naprotiv-menshej-diagonali-romba Аналогично, из прямоугольного треугольника ABO

$AB = \frac{d}{{2\sin \frac{\alpha }{2}}},$

$AO = \frac{d}{2}ctg\frac{\alpha }{2},AC = d \cdot ctg\frac{\alpha }{2},$

${P_{ABCD}} = \frac{{2d}}{{\sin \frac{\alpha }{2}}},$

${S_{ABCD}} = \frac{1}{2} \cdot {d^2}ctg\frac{\alpha }{2},$

$BH = \frac{{d\sin \alpha }}{{2\sin \frac{\alpha }{2}}} = \frac{{d \cdot 2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}}}{{2\sin \frac{\alpha }{2}}} = d\cos \frac{\alpha }{2},$

$r = \frac{1}{2}h,r = \frac{d}{2}\cos \frac{\alpha }{2}.$

Угол, лежащий напротив диагонали ромба

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики