Медианы, проведенные к катетам |

Что можно сказать о прямоугольном треугольнике, в котором известны медианы, проведенные к катетам?

mediana-provedennaya-k-katetu

Медиана, проведённая к катету, разбивает исходный треугольник на два треугольника, один из которых также прямоугольный. Эти треугольники имеют равные площади.

В точке пересечения медианы делятся в отношении 2:1, считая от вершины. Если провести третью медиану, исходный треугольник разбивается на 6 равновеликих треугольников.

Из двух медиан больше та, которая проведена к наименьшей стороне. Таким образом, медиана, проведённая к гипотенузе — наименьшая.

По известным длинам проведённых к катетам медиан можно найти остальные стороны прямоугольного треугольника.

Задача.

В прямоугольном треугольнике медианы, проведенные к катетам, равны m1 и m2. Найти катеты, периметр и площадь этого треугольника.

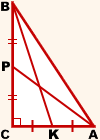mediany-provedennye-k-katetam Дано:∆ABC, ∠C=90º,

AP, CF — медианы, AP=m1, BK=m2

Найти:

$AC,BC,{P_{\Delta ABC}},{S_{\Delta ABC}}.$

Решение:

Для определенности, возьмём BC>AC, следовательно, m1<m2.

Пусть CP=x, CK=y. Так как AP BK — ABC, AC=2x, BC=2y.

Из прямоугольного треугольника ACP по теореме Пифагора

$A{C^2} + C{P^2} = A{P^2},$

$4{x^2} + {y^2} = m_1^2.$

Аналогично, из треугольника BCK

$B{C^2} + C{K^2} = B{K^2},$

$4{y^2} + {x^2} = m_2^2.$

$\left\{ \begin{array}{l} 4{x^2} + {y^2} = m_1^2\\ {x^2} + 4{y^2} = m_2^2 Получили систему уравнений \end{array} \right.$

Умножим второе уравнение системы на -4 и сложим с первым:

$- 15{y^2} = m_1^2 - 4m_2^2$

${y^2} = \frac{{m_1^2 - 4m_2^2}}{{ - 15}} = \frac{{4m_2^2 - m_1^2}}{{15}},$

$y = \sqrt {\frac{{4m_2^2 - m_1^2}}{{15}}} .$

Аналогично, умножив первое уравнение на -4 и сложив со вторым, получаем

$- 15{x^2} = - 4m_1^2 + m_2^2,$

${x^2} = \frac{{4m_1^2 - m_2^2}}{{15}},$

$x = \sqrt {\frac{{4m_1^2 - m_2^2}}{{15}}} .$

$AC = 2\sqrt {\frac{{4m_1^2 - m_2^2}}{{15}}} ,BC = 2\sqrt {\frac{{4m_2^2 - m_1^2}}{{15}}} .$

Из треугольника ABC по теореме Пифагора

$A{B^2} = A{C^2} + B{C^2},$

$A{B^2} = 4\cdot\frac{{4m_1^2 - m_2^2}}{{15}} + 4\cdot\frac{{4m_2^2 - m_1^2}}{{15}} = \frac{{12(m_1^2 + m_2^2)}}{{15}} =$

$= \frac{4}{5}(m_1^2 + m_2^2),$

$AB = 2\sqrt {\frac{{m_1^2 + m_2^2}}{5}} .$

Периметр треугольника ABC равен

${P_{\Delta ABC}} = AB + BC + AC,$

${P_{\Delta ABC}} = 2(\sqrt {\frac{{m_1^2 + m_2^2}}{5}} + \sqrt {\frac{{4m_2^2 - m_1^2}}{{15}}} + \sqrt {\frac{{4m_1^2 - m_2^2}}{{15}}} ),$

площадь —

${S_{\Delta ABC}} = \frac{1}{2} \cdot AC \cdot BC,$

${S_{\Delta ABC}} = \frac{1}{2} \cdot 2\sqrt {\frac{{4m_1^2 - m_2^2}}{{15}}} \cdot 2\sqrt {\frac{{4m_2^2 - m_1^2}}{{15}}} =$

$= \frac{2}{{15}}\sqrt {(4m_1^2 - m_2^2)(4m_2^2 - m_1^2)} .$

Поскольку медиана, проведённая к гипотенузе, равна её половине, можно найти третью медиану как

${m_3} = \frac{1}{2}AB = \sqrt {\frac{{m_1^2 + m_2^2}}{5}} .$

Запоминать эти формулы не нужно, при решении конкретной задачи достаточно повторить эти рассуждения.

Медианы, проведенные к катетам

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики