Теорема Фалеса. Доказательство

Теорема Фалеса. Доказательство

Теорема (Фалеса).

Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.

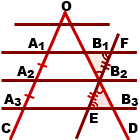
teorema FalesaДано: ∠COD,

A1B1 ∥ A2B2 ∥ A3B3,

A1, A2, A3 ∈OC, B1, B2, B3 ∈OD,

A1A2=A2A3.
Доказать:

B1B2=B2B3.

Доказательство:

teorema Falesa dokazatelstvo

 

1) Через точку B2 проведем прямую EF, EF ∥ A1A3.

2) Рассмотрим четырехугольник A1FB2A2.

— A1F ∥ A2B2 (по условию),

— A1A2 ∥ FB2 (по построению).

Следовательно, A1FB2A2 — параллелограмм (по определению).

По свойству противолежащих сторон параллелограмма, A1A2=FB2.

3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E.

4) Так как A1A2=A2A3 (по условию), то FB2=B2E.

teorema Falesa 8 klass5) Рассмотрим треугольники B2B1F и B2B3E.

— FB2=B2E (по доказанному),

— ∠B1B2F=∠B3B2E (как вертикальные),

— ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF).

Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3.

Что и требовалось доказать.

13 Comments

    1. Пожалуйста! Успехов Вам в усвоении новых знаний! Разобраться в геометрии не так уж и сложно. Главное — делать это систематически.

      Ответить

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *