Медиана, проведенная из прямого угла

В прошлый раз мы доказали утверждение:

Медиана, проведенная из прямого угла к гипотенузе, равна половине гипотенузы.

Рассмотрим еще один способ доказательства, опирающийся на знания материала из курса геометрии только 7 класса.

II способ.

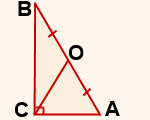 Дано:

∆ABC,

∠BCA=90º,

CO — медиана

Доказать:

   

 Доказательство:

1) На луче СО отложим отрезок OF:

OF=CO.

2) Проведем отрезок AF.

3) Рассмотрим ∆ BOC и  ∆ AOF .

BO=AO (так как CO — медиана по условию)

CO=OF ( по построению)

∠BOC=∠AOF (как вертикальные).

Следовательно, ∆ BOC = ∆ AOF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: CB=AF и соответствующих углов: ∠CBO=∠FAO.

4) ∠CBO=∠FAO. А так как эти углы —  внутренние накрест лежащие при прямых BC и FA и секущей AB, то BC∥FA (по признаку параллельных прямых).

Так как прямая BC перпендикулярна AC, то и FA перпендикулярна AC.

Значит, ∆ ABC и ∆ CFA — прямоугольные.

У них CB=AF (по доказанному), AC — общий катет. Значит, ∆ ABC = ∆ CFA (по двум катетам).

Следовательно, AB=FC. Отсюда

   

Что и требовалось доказать.