Концы диаметра удалены от касательной |

Концы диаметра удалены от касательной

Задача.

Концы диаметра удалены от касательной к окружности на m и n. Найти длину диаметра.

koncy-diametra-ot-kasatelnoj Дано: окружность (O;R),

a — касательная к окружности,

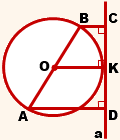
K — точка касания, AB — диаметр,

расстояние от A до a равно m,

расстояние от B до a равно n.

Найти: AB.

Решение:

koncy-diametra-udaleny-ot-kasatelnoj

1) Так как расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из данной точки на данную прямую, m и n — это длины перпендикуляров, опущенных из точек A и B на прямую a.

Проведем

$BC \bot a,AD \bot a,$

AD=m, BC=n.

2) Так как прямые AD и BC перпендикулярны одной прямой a, то они параллельны: AD ∥ BC (по признаку параллельности прямых).

Следовательно, четырехугольник ABCD- трапеция (по определению).

ot-kasatelnoj-do-koncov-diametra 3) Проведём радиус OK.

$OK \bot a$

(как радиус, проведенный в точку касания).

Значит,

$OK\parallel AD\parallel BC.$

4) Так как O — середина диаметра AB, то по теореме Фалеса K — середина CD.

Значит, OK- средняя линия трапеции ABCD.

По свойству средней линии трапеции,

$OK = \frac{{AD + BC}}{2},$

$OK = \frac{{m + n}}{2}.$

5) Так как AB — диаметр, OK- радиус, то

$AB = 2 \cdot OK = 2 \cdot \frac{{m + n}}{2} = m + n.$

Ответ: m+n.

Добавить комментарий Отменить ответ