Если противоположные стороны четырехугольника попарно равны

Теорема (3-й признак параллелограмма).

Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.

 

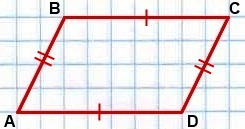
Дано: ABCD — четырехугольник,

AD=BC, AB=CD.

Доказать: ABCD — параллелограмм.

Доказательство:

 

1. Проведем диагональ AC.

2. Рассмотрим треугольники ABC и CDA (важно правильно назвать треугольники!)

1) AB=CD (по условию)

2) BC=AD (по условию)

3) сторона AC- общая

Следовательно, треугольники ABC и CDA равны (по трем сторонам).

3. Из равенства треугольников следует равенство соответствующих углов:

∠CAB=∠ACD и ∠ACB=∠CAD.

4. ∠CAB и∠ACD — внутренние накрест лежащие при прямых AB и CD и секущей AC.

Так как  ∠CAB=∠ACD, то прямые параллельны: AB ∥ CD (по признаку параллельности прямых).

Аналогично, из равенства углов ∠ACB=∠CAD следует параллельность другой пары прямых: AD ∥ BC.

5. Доказали, что в четырехугольнике ABCD

1) AB ∥ CD

2) AD ∥ BC.

Следовательно, ABCD — параллелограмм (по определению).

Что и требовалось доказать.

 

Замечание.

Можно не доказывать параллельность прямых AD и BC.

Из того, что

1) AB=CD (по условию),

2) AB ∥ CD (по доказанному),

следует, что ABCD — параллелограмм (по 2-му признаку).