Биссектрисы параллелограмма |

Если биссектрисы углов параллелограмма, прилежащих к одной стороне перпендикулярны, то биссектрисы противолежащих углов обладают другим свойством.

Свойство биссектрис противоположных углов параллелограмма.

Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.

bissektrisyi protivopolozhnyih uglov parallelogramma

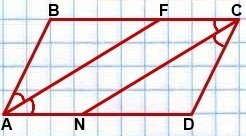
Дано: ABCD — параллелограмм,

AF — биссектриса ∠BAD,

CN- биссектриса ∠BCD.

Доказать: AF ∥ CN или лежат на одной прямой.

Доказательство:

1) Так как AF — биссектриса ∠BAD, CN — биссектриса ∠BCD (по условию), то

$\angle FAD = \frac{1}{2}\angle BAD$

$\angle BCN = \frac{1}{2}\angle BCD.$

Следовательно, их половины тоже равны: ∠FAD=∠BCN.

bissektrisyi protivolezhaschih uglov parallelogramma

Значит, ∠FAD=∠AFB

при BC ∥ AD и секущей BC).

$4)\left. \begin{array}{l} \angle FAD = \angle BCN\\ \angle FAD = \angle AFB \end{array} \right\} \Rightarrow \angle BCN = \angle AFB.$

А так как эти углы — соответственные при прямых AF и CN и секущей BC, то AF ∥ CN (по признаку параллельности прямых).

Если все стороны параллелограмма равны, биссектрисы противоположных углов лежат на одной прямой.

bissektrisyi parallelogramma lezhat na odnoy pryamoy

В этом случае из того, что AB=BC следует, что треугольник ABC — равнобедренный с основанием AC,

а значит, ∠BAC=∠BCA (как углы при основании равнобедренного треугольника).

Что и требовалось доказать.

Биссектрисы параллелограмма