Какой вывод можно сделать из того, что острый угол ромба равен 60 градусам?
Утверждение.
Если острый угол ромба равен 60 градусам, то диагональ равна стороне ромба и делит его на два равных равносторонних треугольника.

Дано:
ABCD — ромб,
∠A=60º,
BD — диагональ.
Доказать: BD=AB,
∆ ABD и ∆ BCD — равносторонние,
∆ ABD = ∆ BCD.
Доказательство:
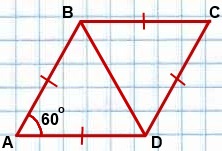
1) Рассмотрим треугольник ABD.
Так как AB=AD (как стороны ромба), то ∆ ABD — равнобедренный с основанием BD.
Углы при основании равнобедренного треугольника
∠ABD=∠ADB=(180º-∠A)/2=(180º-60º)/2=60º.

Поскольку все углы треугольника ABD равны по 60 градусов, то ∆ ABD — равносторонний (по признаку). Следовательно, BD=AB.
2) Треугольники ABD и BCD равны по трем сторонам (AB=BC=CD=AD (как стороны ромба), BD=AB (по доказанному)).
Следовательно, ∆ BCD — равносторонний.
Что и требовалось доказать.
Так как сумма углов ромба, прилежащих к одной стороне, равна 180º, если острый угол ромба равен 60º, его тупой угол равен 120º. Таким образом,
если тупой угол ромба равен 120 градусам, то диагональ равна стороне ромба и делит его на два равных равносторонних треугольника.
