Свойство высот равнобедренного треугольника, проведенных из вершин при основании.
Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.

Дано:
∆ ABC,
AC=BC
AP и BH — высоты.
Доказать: AP=BH
Доказательство:
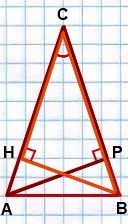
Рассмотрим треугольники ACP и BCH.
1) AC=BC (по условию (как боковые стороны равнобедренного треугольника))
2) ∠C — общий
∠APC=∠BHC=90º (так как AP и BH — высоты (по условию)).
Сумма углов треугольника равна 180º .
В треугольнике ACP
∠CAP=180º — (∠APC+∠C)=180º — 90º — ∠C=90º — ∠C.
В треугольнике BCH
∠CBH=180º — (∠BHC+∠C)=180º — 90º — ∠C=90º — ∠C.
Отсюда,
3) ∠CAP=∠CBH.
Следовательно, треугольники ACP и BCH равны
(по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AP=BH.
Что и требовалось доказать.
Если в треугольнике два угла раны, то этот треугольник — равнобедренный (по признаку).
Если в треугольнике две стороны равны, то этот треугольник — равнобедренный (по определению).
Вывод:
Высоты, проведенные из равных углов треугольника, равны.
Высоты, проведенные к равным сторонам треугольника, равны.
Замечание.
Вместо треугольников ACP и BCH можно было доказать равенство треугольников ABP и BAH.

Но требуют доказать без использования теоремы о сумме углов треугольника в 180 град.
Как вариант, можно использовать признаки равенства прямоугольных треугольников. Треугольники ACP и BCH — прямоугольные: ∠APC=∠BHC=90º (так как AP и BH высоты (по условию). ∆ACP=∆BCH по гипотенузе и острому углу (AC=BC (по условию, как боковые стороны равнобедренного треугольника), ∠C — общий). Следовательно, их соответствующие катеты равны: AP=BH.