Теорема
Угол между хордой и касательной к окружности, проведённой через конец хорды, равен половине дуги, лежащей внутри этого угла.
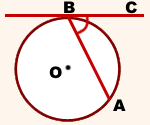 Дано:
Дано:
окр. (O; R), AB — хорда, BC — касательная
Доказать:
![]()
Доказательство:
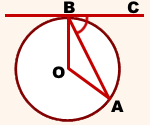 1) Соединим центр окружности с концами хорды.
1) Соединим центр окружности с концами хорды.
Треугольник OAB — равнобедренный с основанием AB (так как OA=OB как радиусы).
Следовательно, ∠OBA=∠OAB (как углы при основании).
По теореме о сумме углов треугольника, ∠OBA+∠OAB+∠AOB=180º. Значит,
![]()
2) ∠OBC=90º (по свойству касательной).
∠ABC=∠OBC-∠OBA
![]()
3) Градусная мера дуги AB равна градусной мере центрального угла AOB.
![]()
отсюда
![]()
Что и требовалось доказать.
Задача
Треугольник ABC вписан в окружность. Через вершину B проведена касательная к окружности, а из точки A на касательную опущен перпендикуляр AF. Найти ∠ACB, если ∠FAB=27º.

Дано: ∆ABC, окр. (O; R) — описанная,
BF — касательная,
![]()
∠FAB=27º
Найти: ∠AСB
Решение:
1) Рассмотрим ∆ABF. ∠AFB=90º. Так как сумма острых углов прямоугольного треугольника равна 90º, то ∠ABF=90º-∠FAB=90-27=63º.
2) ∠ABF — угол между касательной BF и хордой AB. Значит, он равен половине дуги AB:
![]()
3) ∠AСB — вписанный угол, опирающийся на дугу AB. Следовательно он также равен её половине:
![]()
Отсюда, ∠AСB=∠ABF=63º.
Ответ: 63º.
