Прямоугольная трапеция

Что такое прямоугольная трапеция и какими свойствами она обладает?

Определение.

Прямоугольная трапеция — это трапеция, у которой одна боковая сторона перпендикулярна основаниям.

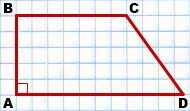
ABCD- прямоугольная трапеция,

AD ∥ BC — основания трапеции,

AB и CD — ее боковые стороны,

$AB \bot AD,AB \bot BC$

Свойства прямоугольной трапеции:

1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.

AB — высота трапеции ABCD.

2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.

∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.

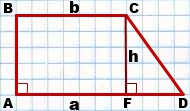
3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.

svojstva-pryamougolnoj-trapecii

$CF \bot AD$

ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.

FCD — прямоугольный треугольник. FD=AD-AF,

отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то

$FD = a - b$

$C{D^2} = C{F^2} + F{D^2},$

$C{D^2} = {h^2} + {(a - b)^2}$

4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.

pryamougolnaya-trapeciya-svojstva Треугольник ABC — прямоугольный.

По теореме Пифагора,

$A{C^2} = A{B^2} + B{C^2},$

$A{C^2} = {h^2} + {b^2}$

$AC = \sqrt {{h^2} + {b^2}}$

5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.

opredelenie-pryamougolnoj-trapecii Треугольник ABD — прямоугольный.

По теореме Пифагора,

$B{D^2} = A{B^2} + A{D^2},$

$B{D^2} = {a^2} + {h^2}$

$BD = \sqrt {{a^2} + {h^2}}$