Теорема (Признак равнобедренного треугольника)
Если в треугольнике два угла равны, то этот треугольник — равнобедренный.

Дано:
∆ ABC,
∠A=∠B
Доказать:
∆ ABC — равнобедренный.
Доказательство:
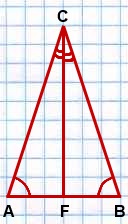
Проведем биссектрису CF.

Рассмотрим треугольники ACF и BCF.
1) ∠ACF=∠BCF (так как CF — биссектриса (по построению))
2) CF — общая сторона
∠A=∠B (по условию)
Сумма углов треугольника равна 180º.
В треугольнике ACF
∠AFC=180º — (∠A+∠ACF).
В треугольнике BCF
∠BCF =180º — (∠B+∠BCF).
Из 180º вычли сумму равных углов. Получили равные углы:
![]()
Таким образом, имеем:
3)∠AFC=∠BFC.
Следовательно, ∆ACF = ∆BCF (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AC=BC.
Значит, треугольник ABC — равнобедренный с основанием AB (по определению равнобедренного треугольника).
Что и требовалось доказать.
Данный признак равнобедренного треугольника можно доказать другими способами.
2 способ
Рассмотрим треугольники ABC и BAC.
(это — два разных треугольника. Подробнее — смотрите «Два треугольника равны«)
1) AB=BA (по условию)
2) ∠A=∠B (по условию)
3) ∠B =∠A (по условию)
Следовательно, ∆ACF = ∆BCF (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: AC=BC.
Вывод: ∆ ABC — равнобедренный с основанием AB.
3 способ
По соотношениям между углами треугольника и противолежащими сторонами, в треугольнике против б’ольшего угла лежит б’ольшая сторона. Следствие: против равных углов лежат равные стороны. Таким образом, если в треугольнике два угла равны, то лежащие напротив этих углов стороны тоже равны, а значит, треугольник — равнобедренный.
