Диаметр делит хорду пополам |

Если диаметр делит хорду пополам, каково их взаимное расположение?

Утверждение

Если диаметр делит хорду пополам, то он перпендикулярен этой хорде.

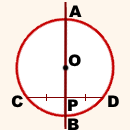diametr-delit-hordu-popolam Дано: окружность (O;R),

AB — диаметр, CD — хорда,

CD ∩ AB=P, CP=PD.

Доказать:

$CD \bot AB.$

Доказательство:

diametr-prohodit-cherez-seredinu-hordy Соединим концы хорды CD с точкой O — центром окружности.

Так как OC=OD (как радиусы), то треугольник COD — равнобедренный с основанием CD.

Так как CP=PD, то OP — медиана треугольника COD, проведённая к основанию.

По свойству равнобедренного треугольника, OP является также его высотой.

Следовательно,

$CD \bot OP,$

а значит, и

$CD \bot AB.$

Что и требовалось доказать.

Диаметр делит хорду пополам