Теорема (1-й признак параллелограмма).
Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник — параллелограмм.
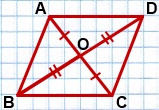 Дано: ABCD — четырехугольник,
Дано: ABCD — четырехугольник,
AC и BD — диагонали,
AC∩BD=O,
AO=OC, BO=OD.
Доказать: ABCD — параллелограмм.
Доказательство:
1. Рассмотрим треугольники AOD и COB.
1) AO=OC (по условию);
2) BO=OD (по условию);
3)∠AOD=∠COB (как вертикальные).
Следовательно, треугольники AOD и COB равны (по двум сторонам и углу между ними).
2. Из равенства треугольников следует равенство соответствующих углов:∠ADO=∠CBO.
А так как эти углы — внутренние накрест лежащие при прямых AD и BC и секущей BD, то AD∥BC (по признаку параллельных прямых).
3. Аналогично, ∆ AOB=∆ COD, ∠ABO=∠CDO и AB∥CD.
4. Доказали, что AD∥BC и AB∥CD.
Значит, ABCD — параллелограмм (по определению).
