Биссектриса равностороннего треугольника

Какими свойствами обладает биссектриса равностороннего треугольника? Как, зная сторону правильного треугольника, найти его биссектрису? Чему равна длина биссектрисы через радиус вписанной и описанной окружностей?

Теорема 1

(свойство биссектрисы равностороннего треугольника)

В равностороннем треугольнике биссектриса, проведённая к любой стороне, является также его медианой и высотой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

Так как AB=BC, треугольник ABC — равнобедренный с основанием AC.

Проведем биссектрису BF.

По свойству равнобедренного треугольника, BF является также его медианой и высотой.

Аналогично, треугольник ABC — равнобедренный с основанием BC, треугольник ABC — равнобедренный с основанием AB, а его биссектрисы AK и CD  — еще и медианы и высоты.

Что и требовалось доказать.

Теорема 2

(свойство биссектрис равностороннего треугольника)

Все три биссектрисы равностороннего треугольника равны между собой.

Доказательство:

Пусть в треугольнике ABC AB=BC=AC.

AK, BF CD — биссектрисы треугольника ABC.

В треугольниках ABF, BCD и CAK:

• AB=BC=CA (по условию)
• ∠BAF=∠CBD=∠ACK (как углы равностороннего треугольника)
• ∠ABF=∠BCD=∠CAK (как как AK, BF CD — биссектрисы равных углов).

Значит, треугольники ABF, BCD и CAK равны (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AK=BF=CD.

Что и требовалось доказать.

Из теорем 1 и 2 следует, что в равностороннем треугольнике все биссектрисы, медианы и высоты равны между собой.

1) Найдём биссектрису равностороннего треугольника через его сторону.

В треугольнике ABC AB=BC=AC=a.

BF — биссектриса, BF=l.

По свойствам равностороннего треугольника,  BF — высота ∆ ABC, ∠A=60º.

Из прямоугольного треугольника ABF по определению синуса

   

   

Таким образом, формула биссектрисы равностороннего треугольника по его стороне:

   

2) Найдём биссектрису равностороннего треугольника через радиусы вписанной и описанной окружностей.

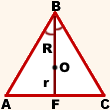В правильном треугольнике ABC центры вписанной и описанной окружностей совпадают.

Центр вписанной окружности — точка пересечения биссектрис треугольника. Биссектрисы равностороннего треугольника также являются его медианами. Медианы треугольника в точке пересечения делятся в отношении 2 к 1, считая от вершины.

Следовательно, точка O — центр вписанной и описанной окружностей, OF — радиус вписанной окружности, OF=r, BO — радиус описанной окружности, BO=R и BO:OF=2:1.

Отсюда,

   

   

Таким образом, длина биссектрисы через радиус вписанной окружности равна

   

через радиус описанной окружности —