Второй признак подобия треугольников

Теорема

(Второй признак подобия треугольников — подобие треугольников по двум пропорциональным сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

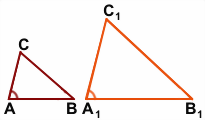Дано: ΔABC, ΔA₁B₁C₁,

∠A=∠A₁,

   

Доказать: ΔABC∼ ΔA₁B₁C₁

Доказательство:

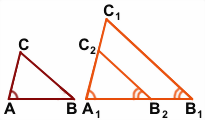1) Отложим на луче A₁B₁ отрезок A₁B₂, A₁B₂=AB.

2) Через точку B₂ проведём прямую B₂С₂, параллельную прямой B₁C₁.

3) ∠A₁B₂C₂=∠A₁B₁C₁ (как соответственные при B₂C₂ ∥ B₁C₁ и секущей A₁B₁).

4) В треугольниках A₁B₂C₂ и A₁B₁C₁:

• ∠A₁ — общий
• ∠A₁B₂C₂=∠A₁B₁C₁ (по доказанному)

Поэтому  ΔA₁B₂C₂∼ΔA₁B₁C₁ (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

5) Так как A₁B₂=AB и

   

то AC=A₁C₂.

6) В треугольниках ABC и A₁B₂C₂:

• A₁B₂=AB (по построению)
• AC=A₁C₂ (по доказанному)
• ∠A=∠A₁ (по условию).

Поэтому ΔABC=ΔA₁B₂C₂ (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих углов: ∠ABC=∠A₁B₂C₂.

7) Так как ∠A₁B₂C₂=∠A₁B₁C₁, то и ∠ABC=∠A₁B₁C₁.

8) В треугольниках ABC и A₁B₁C₁:

• ∠A=∠A₁ (по условию);
• ∠ABC=∠A₁B₁C₁ (по доказанному).

Следовательно, ΔABC∼ ΔA₁B₁C₁(по двум углам).

Что и требовалось доказать.