В равнобедренном треугольнике углы при основании равны

Теорема (свойство углов при основании равнобедренного треугольника).

В равнобедренном треугольнике углы при основании равны.

 

Дано: ∆ ABC,

AC=BC

Доказать: ∠A=∠B.

 

 

Доказательство:

 

 

Проведем в треугольнике ABC

биссектрису CF.

 

 

 

 

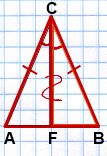
Рассмотрим ∆ ACF и ∆ BCF.

1) AC=BC (по условию)

2) CF — общая сторона

3) ∠ACF=∠BCF (так как CF — биссектриса).

 

 

Следовательно, ∆ ACF=∆ BCF (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих углов: ∠A=∠B.

Что и требовалось доказать.

 

И обратно: если два угла треугольника равны, то этот треугольник — равнобедренный.

Эта теорема, обратная свойству углов при основании равнобедренного треугольника, относится к одному из признаков равнобедренного треугольника. Ее мы докажем позже.