Осевая симметрия

Осевая симметрия — это симметрия относительно прямой.

Пусть дана некоторая прямая g.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

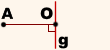1) Провести из точки A к прямой g перпендикуляр AO.

 

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Прямая g называется осью симметрии.

Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.

Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.

Преобразование фигуры F  в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.

Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.

Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.

Примеры фигур, симметричных относительно прямой.

1) Прямоугольник.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

2) Ромб.

Ромб имеет две оси симметрии:

прямые, на которых лежат его диагонали.

3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.

4) Окружность.

Окружность имеет бесконечное множество осей симметрии:

любая прямая, содержащая диаметр, является осью симметрии окружности.

5) Прямая.

Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.

6) Равнобедренная трапеция.

Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.

7) Равнобедренный треугольник.

Равнобедренный треугольник имеет одну ось симметрии:

прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

 

8) Равносторонний треугольник.

Равносторонний треугольник имеет три оси симметрии:

прямые, содержащие его высоты (медианы, биссектрисы).

 

9) Угол.

Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.

 

Теорема.

Осевая симметрия является движением.