Какими могут быть углы треугольника? Могут ли быть все углы треугольника острыми? Тупыми? Прямыми? Могут ли все углы треугольника быть равными? Ответы на эти вопросы можно получить с помощью теоремы о сумме углов треугольника.
Острый угол — это угол с градусной мерой от 0º до 90º.
Прямой угол — это угол, величина которого равна 90º.
Тупой угол — это угол, градусная мера которого может изменяться от 90ºдо 180º.
По теореме о сумме углов треугольника, сумма углов треугольника равна 180º.
Может ли в треугольнике быть два тупых угла?
Поскольку градусная мера тупого угла больше 90º, сумма двух тупых углов больше180º. Сумма углов треугольника равна 180º, поэтому двух тупых углов в треугольнике быть не может.
Может ли в треугольнике быть два прямых угла?
Так как градусная мера прямого угла равна 90º, сумма двух прямых углов равна 180º. Сумма всех трех углов треугольника — 180º, значит, двух прямых углов в треугольнике быть не может.
Тем более, все три угла треугольника не могут быть прямыми или тупыми.
А вот острыми все три угла треугольника могут быть. И равными между собой — тоже.
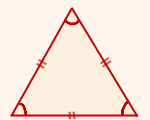 Если все углы треугольника равны, чтобы их найти, делим 180ºна 3:
Если все углы треугольника равны, чтобы их найти, делим 180ºна 3:
180:3= 60º .
Если у треугольника все углы равны, то и все стороны тоже равны.
Такой треугольник называется равносторонним или правильным.
Более того, у любого треугольника острых углов — не меньше двух (если предположить, что острых углов меньше двух, то два не острых в сумме дают 180º или больше, что противоречит теореме о сумме углов треугольника).
Могут ли углы треугольника быть равными 23º, 78º и 79º?
Проверяем выполнение теоремы о сумме углов треугольника: 23º+78º+79º=180º. Получили верное равенство. Значит, треугольник с такими углами существует.
