Какими свойствами обладает биссектриса внешнего угла равнобедренного треугольника?
Утверждение 1.
Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.
Утверждение 2.
Биссектриса внешнего угла при вершине равнобедренного треугольника:
1) делит внешний угол на два угла, каждый из которых равен углу при основании;
1) параллельна основанию.
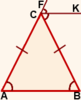
Дано: ∆ ABC,
AC=BC,
∠BCF — внешний угол при вершине C,
CK — биссектриса ∠BCF.
Доказать:
1)∠BCK=∠KCF=∠A;
2) CK ∥ AB.
Доказательство:
1) Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним, то
∠BCF=∠A+∠B.
Так как треугольник ABC — равнобедренный с основанием AB, то ∠A=∠B.
Следовательно, ∠BCF=2∠A.
Так как CK — биссектриса ∠BCF, то она делит его на два равных угла.
Таким образом, ∠BCK=∠KCF=∠A.
2) ∠BCK=∠A (по доказанному).
А так эти углы — внутренние накрест лежащие при прямых CK и AB и секущей BC, то
CK ∥ AB (по признаку параллельных прямых).
Что и требовалось доказать.