Задачи на второй признак равенства треугольников

Рассмотрим некоторые задачи на второй признак равенства треугольников.

1)

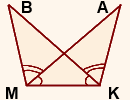     Дано:

∠AMK=∠BKM,

∠AKB=∠BMA

Доказать: ∆AKM=∆BMK.

Сначала проведем анализ задачи.

    Выделим треугольники, равенство которых надо доказать, разными цветами.

Цветовая визуализация сразу же дает подсказку — треугольники имеют общую сторону MK.

Кроме того, по условию, данные треугольники имеют равные углы AMK и BKM.

Для доказательства равенства треугольников не хватает равенства еще одной пары элементов.

В условии сказано, что углы AKB и BMA равны. Угол AKM равен сумме углов AKB и BKM, угол BMK —  сумме углов BMA и AMK. Если к равным углам прибавить равные углы, то получим равные углы. Значит, углы AKM и BMK равны.

Теперь запишем доказательство.

Доказательство:

Рассмотрим ∆AKM и ∆BMK.

1) MK — общая сторона.

2) ∠AMK=∠BKM (по условию).

 

 

Следовательно, ∆AKM=∆BMK (по стороне и двум прилежащим к ней углам, то есть, по второму признаку равенства треугольников).

Что и требовалось доказать.

2)

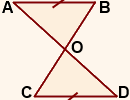     Дано:

AB∥CD,

AB=CD

Доказать: ∆AOB=∆DOC.

Анализ задачи.

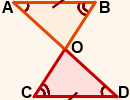Выделим треугольники AOB и DOC разными цветами.

По условии, данные треугольники имеют одну пару равных элементов — стороны AB и CD равны.

Видим пару равных вертикальных углов AOB и DOC. Однако, они нам не подходят — раз равные стороны AB и CD, углы должны быть рядом с ними.

Чтобы определить равные углы этих треугольников, можно воспользоваться подсказкой.

Так как прямые AB∥CD, ищем и находим две пары равных внутренних накрест лежащих углов.

Все три пары равных элементов для второго признака равенства треугольников имеются. Теперь можно перейти к записи доказательства.

Доказательство:

1) AB=CD (по условию).

2) ∠ABO=∠DCO (как накрест лежащие при AB∥CD и секущей BC).

3) ∠BAO=∠CDO (как накрест лежащие при AB∥CD и секущей AD).

Следовательно, ∆AOB=∆DOC (по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.

3)

     Дано:

∆CFD — равнобедренный с основанием CD,

∠AFC=∠BFD

Доказать: ∆AFB — равнобедренный.

Анализ задачи:

    Чтобы доказать, что треугольник AFB — равнобедренный, нужно доказать либо равенство двух его сторон: AF=BF, либо равенство двух углов: ∠A=∠B.

Равенство сторон и углов следует из равенства треугольников.

Значит, нужно доказать равенство пары треугольников со сторонами AF и BF и углами A и B. Подходят треугольники AFC и BFD.

Выделим эти треугольники разными цветами.

Их углы AFC и BFD равны по условию. Также из условия известно, что ∆CFD — равнобедренный с основанием CD. Из этого следует, что его боковые стороны CF и DF равны и углы при основании равны ∠FCD=∠FDC. Равенство сторон CF и DF можно использовать для доказательства равенства треугольников AFC и BFD, а что делать с углами?

Углы ACF и BDF смежные с углами FCD и FDC. А так как ∠FCD=∠FDC, то и смежные с ними углы ACF и BDF тоже равны.

Три пункта для второго признака равенства треугольников получили. Переходим к записи доказательства.

Доказательство:

Рассмотрим треугольники  AFC и BFD.

1) ∠AFC =∠BFD (по условию).

2) CF=DF (как боковые стороны равнобедренного треугольника CFD).

3) ∠ACF=∠BDF (как смежные с равными углами: ∠FCD=∠FDC как углы при основании равнобедренного треугольника CFD).

Следовательно, ∆AFC = ∆BFD (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: AF=BF. Значит, ∆AFB — равнобедренный с основанием AB (по определению равнобедренного треугольника).

Что и требовалось доказать.