Задачи на первый признак равенства треугольников

Рассмотрим конкретные задачи на первый признак равенства треугольников.

1)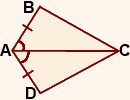 Дано:

AB=AD,

∠BAC=∠DAC

Доказать: ∆ABC=∆ADC

Доказательство:

Выделим треугольники, равенство которых надо доказать, разными цветами.

Этот ход сразу позволяет увидеть, что данные треугольники имеют общую сторону AC.

Теперь запишем равные пары элементов.

 

1) AB=AD (по условию)

2) ∠BAC=∠DAC (по условию)

3) AC — общая сторона.

Следовательно, ∆ABC=∆ADC (по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников).

Что и требовалось доказать.

2)

  Дано:

AO=BO,

CO=DO

Доказать: ∆AOC=∆BOD.

Доказательство:

Выделим треугольники, равенство которых доказываем, разными цветами.

Определяем те элементы, о равенстве которых известно по условию задачи:

1)  AO=BO (по условию)

2) CO=DO (по условию).

Для равенства треугольников осталось найти третью пару равных элементов. Это — углы AOC и BOD.

3) ∠AOC = ∠BOD (как вертикальные).

Все три пункта первого признака равенства треугольников есть. Следовательно, ∆AOC=∆BOD (по двум сторонам и углу между ними).

Что и требовалось доказать.

3)

  Дано:

AB=AC,

AF=AK

Доказать: ∆ABK=∆ACF

Доказательство:

Выделяем треугольники ABK  и ACF разными цветами.

Цветовая визуализация позволяет увидеть, что для данных треугольников угол A — общий .

Далее определяем, равенство каких элементов дано в условии. Записываем доказательство.

1) AB=AC (по условию)

2) AF=AK (по условию)

3) ∠A — общий.

Все три пункта первого признака равенства треугольников выполнены.

Следовательно, ∆ABK=∆ACF (по двум сторонам и углу между ними).

Что и следовало доказать.

 

В следующий раз рассмотрим задачи на второй признак равенства треугольников.