Высоты в остроугольном треугольнике

В любом треугольнике все три высоты пересекаются в одной точке. Все высоты в остроугольном треугольнике лежат внутри треугольника (как и точка пересечения высот).

Задача.

Высоты BB₁ и CC₁ остроугольного треугольника ABC пересекаются в точке E. Доказать, что углы BB₁C₁ и BCC₁ равны; углы B₁C₁С и BB₁C равны.

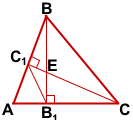Дано: ΔABC — остроугольный,

BB₁⊥AC, CC₁⊥AB, BB₁∩CC₁=E

Доказать: ∠BB₁C₁=∠BCC₁;

2)∠B₁C₁С=∠BB₁C

Доказательство:

Около любого треугольника можно описать окружность. Центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы. Радиус такой окружности равен половине гипотенузы.

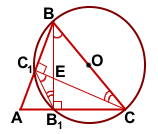Центр описанной около прямоугольного треугольника BB₁C окружности лежит на середине гипотенузы BC, радиус этой окружности равен половине BC.

Центр описанной около прямоугольного треугольника BCC₁ окружности — середина гипотенузы BC, радиус равен половине BC.

Значит эти треугольники вписаны в одну и ту же окружность.

Следовательно, точки B, C, B₁ и C₁лежат на одной окружности.

Отсюда:

∠BB₁C₁=∠BCC₁ (как вписанные углы, опирающиеся на одну дугу BC₁);

∠B₁C₁С=∠B₁BC (как вписанные углы, опирающиеся на одну дугу B₁C).

Что и требовалось доказать.

То есть решение такого рода задач начинаем с поиска прямоугольных треугольников с общей гипотенузой.