Если высота ромба делит его сторону пополам, то что можно сказать о свойствах такого ромба?
 Рассмотрим ромб ABCD.
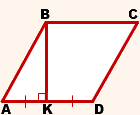
Рассмотрим ромб ABCD.
В нём высота BK делит
сторону AD пополам
(то есть AK=DK).
Проведем диагональ BD.
 Рассмотрим треугольник ABD.
Рассмотрим треугольник ABD.
В нём BK — высота и медиана (так как AK=DK).
Значит, треугольник ABD — равнобедренный с основанием AD (по признаку).
Следовательно, AB=BD.
Но AB=AD (как стороны ромба).
Получили, что AB=BD=AD, то есть треугольник ABD — равносторонний.
Поэтому все его углы равны по 60º. Значит, острый угол ромба равен 60º:∠BAD=60º.
Треугольник BCD в этом случае также равносторонний.
Вывод:
Если высота ромба делит его сторону пополам, то
— меньшая диагональ ромба равна стороне ромба;
— меньшая диагональ делит ромб на два равносторонних треугольника;
