Вписанный прямой угол

Вписанный прямой угол обладает свойством, непосредственно вытекающим из теоремы о вписанном угле.

Утверждение

Вписанный прямой угол опирается на диаметр.

(другой вариант:

вписанный прямой угол опирается на полуокружность).

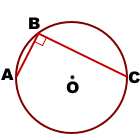vpisannyj-pryamoj-ugol Дано: окружность (O;R), ∠ABC — вписанный угол,

∠ABC=90º

Доказать: AC — диаметр

Доказательство:

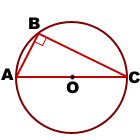vpisannyj-ugol-pryamoj Вписанный угол равен половине соответствующего ему центрального угла,

$\angle ABC = \frac{1}{2}\angle AOC.$

А так как ∠ABC=90º,

$\angle AOC = 2 \cdot \angle ABC,$

$\angle AOC = 2 \cdot {90^o} = {180^o}.$

Следовательно, точки A, C и O лежат на одной прямой, то есть отрезок AC соединяет две точки окружности и проходит через её центр.

Значит, хорда AC является диаметром окружности ( а дуга AC — полукругом).

Что и требовалось доказать.