Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
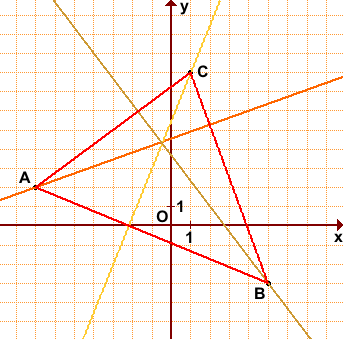
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
![]()
Таким образом, уравнение прямой BC —
![]()
Угловой коэффициент прямой, перпендикулярной BC,
![]()
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
![]()
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
![]()
Итак, уравнение высоты, проведённой к стороне BC:
![]()
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
![]()
Уравнение прямой AB:
![]()
Угловой коэффициент перпендикулярной ей прямой
![]()
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
![]()
Угловой коэффициент прямой, перпендикулярной AC,
![]()
Таким образом, уравнение перпендикулярной AC прямой имеет вид
![]()
Подставив в него координаты точки B(5;-3), найдём b:
![]()
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
![]()

Доброе утро. Спасибо!