Площадь треугольника по стороне

Чтобы найти площадь треугольника по одной стороне, нужно знать также высоту, проведенную к этой стороне.

Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.

Формула площади треугольника:

formula ploschadi treugolnika cherez storonu

$S = \frac{1}{2}a{h_a}$

(индекс a внизу буквы h указывает, что высота проведена к стороне a), или просто

$S = \frac{1}{2}ah.$

ploschad treugolnika po storone

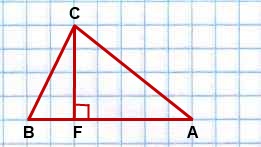
Дано:

∆ ABC,

$CF \bot AB.$

Доказать:

${S_{\Delta ABC}} = \frac{1}{2}AB \cdot CF.$

Доказательство:

ploschad treugolnika cherez storonu

1) Проведем через вершину C треугольника прямую, параллельную стороне AB, через вершину A — прямую, параллельную стороне BC.

Обозначим точку пересечения этих прямых через D.

2) Четырехугольник ABCD — параллелограмм (по определению).

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне:

${S_{ABCD}} = AB \cdot CF.$

3) Рассмотрим треугольники ABC и CDA.

Сторона AC — общая.

Следовательно, треугольники ABC и CDA равны (по трем сторонам).

Равные фигуры имеют равные площади:

${S_{\Delta ABC}} = {S_{\Delta CDA}},$

${S_{ABCD}} = 2{S_{\Delta ABC}}.$

Отсюда, площадь треугольника ABC равна половине площади параллелограмма ABCD, то есть

${S_{\Delta ABC}} = \frac{1}{2}AB \cdot CF.$

Что и требовалось доказать.

Часто сторону треугольника, к которой проведена высота, называют основанием.

В этом случае формулировка правила для нахождения площади треугольника звучит немного иначе:

Площадь треугольника равна половине произведения его площади основания на высоту.