Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

$O{A_1} = k \cdot OA,$

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

gomotetiya — *гомотетия с коэффициентом k>0*

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

$O{A_1} = k \cdot OA$

$O{B_1} = k \cdot OB$

$O{C_1} = k \cdot OC$

$O{D_1} = k \cdot OD$

и соединить вершины A1, B1, C1и D1 отрезками.

При k<0 гомотетия называется обратной ( точки A и A1лежат по разные стороны от точки O).

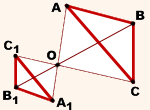
gomotetichnye-figury — *гомотетия с коэффициентом k<0*

Чтобы построить треугольник, гомотетичный данному треугольнику ABC с центром гомотетии в точке O и коэффициентом k, k<0, нужно провести лучи, выходящие из вершин треугольника, проходящие через точку O, отложить на них отрезки соответствующей длины:

$O{A_1} = k \cdot OA$

$O{B_1} = k \cdot OB$

$O{C_1} = k \cdot OC$

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

При k= -1 гомотетия является симметрией относительно центра O (то есть центральная симметрия является частным случаем гомотетии).

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Гомотетия

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики