Теорема о пропорциональных отрезках |

Как теорема о пропорциональных отрезках применяется при решении задач?

Теорема о пропорциональных отрезках.

Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

teorema o proportsionalnyih otrezkah

$\frac{{O{A_1}}}{{O{A_2}}} = \frac{{O{B_1}}}{{O{B_2}}}$

Если параллельных прямых больше, то и количество пропорциональных отрезков увеличивается. Например,

zadacha teorema o proportsionalnyih otrezkah

$\frac{{AB}}{{AD}} = \frac{{AC}}{{AE}},\frac{{AB}}{{AF}} = \frac{{AC}}{{AK}},$

$\frac{{AB}}{{AF}} = \frac{{AC}}{{AK}},\frac{{AB}}{{AP}} = \frac{{AC}}{{AT}},$

$\frac{{BD}}{{BF}} = \frac{{CE}}{{CK}},\frac{{DF}}{{DP}} = \frac{{EK}}{{ET}},$

$\frac{{DF}}{{FP}} = \frac{{EK}}{{KT}},\frac{{BD}}{{DF}} = \frac{{CE}}{{EK}}$

и т.д.

Рассмотрим задачи на применение теоремы оп пропорциональных отрезках.

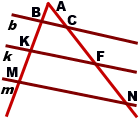zadacha na teoremu o proportsionalnyih otrezkah Дано: ∠A,

b ∥ k ∥ m,

AC=4, FN=8,

BK=5, KM=6.

Найти: AB, CF.

Решение:

По теореме о пропорциональных отрезках,

$\frac{{BK}}{{KM}} = \frac{{CF}}{{FN}},$

$\frac{5}{6} = \frac{{CF}}{8}, \Rightarrow CF = \frac{{5 \cdot \mathop {\overline 8 }\limits^4 }}{{\mathop {\underline 6 }\limits_3 }} = \frac{{20}}{3} = 6\frac{2}{3}.$

Снова применяем теорему о пропорциональных отрезках:

$\frac{{AB}}{{BK}} = \frac{{AC}}{{CF}},$

$\frac{{AB}}{5} = \frac{4}{{\frac{{20}}{3}}}, \Rightarrow AB = \frac{{5 \cdot 4}}{{\frac{{20}}{3}}} = \frac{{5 \cdot 4 \cdot 3}}{{20}} = 3.$

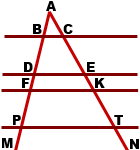2) zadacha na teoremu o proportsionalnyih otrezkah Дано: ∠MAN,

BC ∥ DE ∥ FK ∥ PT,

BD=20, DF=5, EK=6, KT=21.

Найти:CE, FP.

Решение:

По теореме о пропорциональных отрезках:

$\frac{{BD}}{{DF}} = \frac{{CE}}{{EK}},\frac{{20}}{5} = \frac{{CE}}{6}, \Rightarrow CE = \frac{{20 \cdot 6}}{5} = 24,$

$\frac{{DF}}{{FP}} = \frac{{EK}}{{KT}},\frac{5}{{FP}} = \frac{6}{{21}}, \Rightarrow FP = \frac{{5 \cdot 21}}{6} = 17,5.$

Теорема о пропорциональных отрезках

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики