Серединный перпендикуляр

Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?

Определение.

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

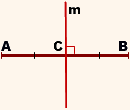
m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

   

   

 

 

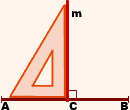
Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

 

 

 

 

Свойства серединного перпендикуляра.

1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

 

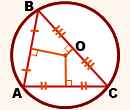
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.

 

3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.