Биссектрисы смежных углов | Треугольники

Биссектрисы смежных углов

Зависит ли угол, который образуют между собой биссектрисы смежных углов, от градусных мер этих углов?

Утверждение.

Биссектрисы смежных углов перпендикулярны.

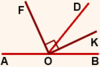
bissektrisyi smezhnyih uglov  Дано:  ∠AOD и ∠DOB — cмежные,

OF — биссектриса ∠AOD,

OK — биссектриса ∠DOB

Доказать:

    \[OF \bot OK\]

Доказательство:

Так как сумма смежных углов равна 180º, то ∠AOD+∠DOB=180º.

Так как OF — биссектриса ∠AOD, то

    \[\angle FOD = \frac{1}{2}\angle AOD.\]

Так как OK — биссектриса ∠DOB, то

    \[\angle DOK = \frac{1}{2}\angle DOB.\]

Отсюда,

    \[\angle FOD + \angle DOK = \frac{1}{2}\angle AOD + \frac{1}{2}\angle DOB = \]

    \[ = \frac{1}{2}(\angle AOD + \angle DOB) = \frac{1}{2} \cdot {180^o} = {90^o}.\]

 

bissektrisyi smezhnyih uglov perpendikulyarnyi Таким образом, мы доказали, что угол между биссектрисами смежных углов не зависит от градусной меры смежных углов и всегда равен 90º, то есть, биссектрисы смежных углов перпендикулярны.

 

Задача.

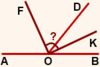ugol mezhdu bissektrisami smezhnyih uglov   Найти угол между биссектрисами смежных углов, один из которых на 100º больше другого.

 

 

Решение:

Так как биссектрисы смежных углов перпендикулярны, ∠FOK=90º.

(Находить градусные меры смежных углов не требуется).

Ответ: 90º.

Добавить комментарий