Коллинеарные векторы |

Какие векторы называются коллинеарными?

Какими свойствами обладают коллинеарные векторы?

Определение

Векторы называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.

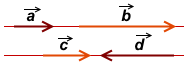kollinearnye-vektory Например, все векторы

$\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow d$

коллинеарны между собой.

Нулевой вектор считают коллинеарным любому вектору.

Коллинеарные векторы делятся на сонаправленные и противоположно направленные.

Определение

Векторы

$\overrightarrow {AB}$

$\overrightarrow {CD}$

называются сонаправленными (или одинаково направленными), если лучи AB и CD сонаправлены.

(Сонаправленность векторов записывают с помощью знака ↑↑).

Например,

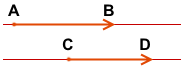
sonapravlennye-vektory

$\overrightarrow {AB} \uparrow \uparrow \overrightarrow {CD}$

Определение

Векторы

$\overrightarrow {AB}$

$\overrightarrow {CD}$

называются противоположно направленными, если лучи AB и CD противоположно направлены.

(Противоположное направление векторов обозначают знаком ↑↓).

Например,

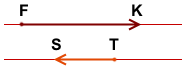
protivopolozhno-napravlennye-vektory

$\overrightarrow {FK} \uparrow \downarrow \overrightarrow {ST}$

Теорема

(Свойство коллинеарных векторов)

У коллинеарных векторов соответствующие координаты пропорциональны

То есть если векторы

$\overrightarrow a (a_1 ;a_2 )$

$\overrightarrow b (b_1 ;b_2 )$

коллинеарны, то

$\frac{{a_1 }}{{b_1 }} = \frac{{a_2 }}{{b_2 }}.$

Теорема

(Признак коллинеарных векторов)

Если соответствующие координаты векторов пропорциональны, то эти векторы коллинеарны.

То есть если

$\frac{{a_1 }}{{b_1 }} = \frac{{a_2 }}{{b_2 }},$

то векторы

$\overrightarrow a (a_1 ;a_2 )$

$\overrightarrow b (b_1 ;b_2 )$

коллинеарны.

Причем

$\frac{{a_1 }}{{b_1 }} = \frac{{a_2 }}{{b_2 }} = \lambda$

при λ>0 векторы сонаправлены

$\overrightarrow a \uparrow \uparrow \overrightarrow b ,$

при λ<0 — противоположно направлены.

Теорема

(О разложении вектора по двум неколлинеарным векторам)

Если векторы

$\overrightarrow a$

$\overrightarrow b$

неколлинеарны, то любой вектор

$\overrightarrow c$

можно разложить как

$\overrightarrow c = m\overrightarrow a + n\overrightarrow b ,$

где m и n — некоторые числа.

Такое разложение единственно.

Коллинеарные векторы

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики