Умножение вектора на число |

Определение

Произведением вектора

$\overrightarrow {\rm{a}} (a_1 ;a_2 )$

на число k называется такой вектор

$k\overrightarrow {\rm{a}} ,$

длина которого равна

$\left| k \right| \cdot \left| {\overrightarrow a } \right|,$

причем при k>0 этот вектор сонаправлен с вектором a, при k<0 — противоположно направлен:

$k > 0 \Rightarrow k\overrightarrow {\rm{a}} \uparrow \uparrow \overrightarrow a ,$

$k < 0 \Rightarrow k\overrightarrow {\rm{a}} \uparrow \downarrow \overrightarrow a .$

Например,

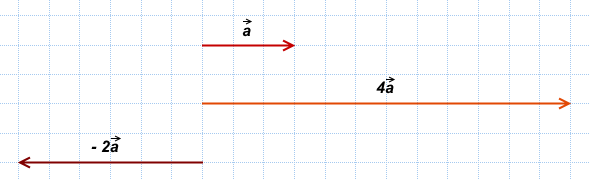
umnozhenie-vektora-na-chislo

Чтобы найти координаты вектора

$k\overrightarrow a ,$

надо каждую координату вектора

$\overrightarrow a (a_1 ;a_2 )$

умножить на число k:

$k \cdot \overrightarrow a = (\overrightarrow {ka_1 ;ka_2 } )$

Примеры:

Дано:

$\overrightarrow a (2; - 7),$

$\overrightarrow b ( - 5;0),$

$\overrightarrow c (10;9).$

Найти:

$1)4\overrightarrow a ;$

$2) - 3\overrightarrow {b;}$

$3)\frac{2}{3}\overrightarrow {c;}$

$4)5\overrightarrow a + 9\overrightarrow b ;$

$5)6\overrightarrow b - 8\overrightarrow c .$

Решение:

1) Чтобы найти координаты вектора

$4\overrightarrow a ,$

надо умножить на 4 каждую координату вектора a:

$4\overrightarrow a = 4 \cdot (\overrightarrow {2; - 7} ) = (\overrightarrow {4 \cdot 2;4 \cdot ( - 7)} ) = (\overrightarrow {8; - 28} ).$

2) Аналогично выполняем умножение вектора b на число -3:

$- 3\overrightarrow b = - 3 \cdot (\overrightarrow { - 5;0} ) = (\overrightarrow { - 3 \cdot ( - 5); - 3 \cdot 0} ) = (\overrightarrow {15;0} ).$

$3)\frac{2}{3}\overrightarrow c = \frac{2}{3} \cdot (\overrightarrow {10;9} ) = (\overrightarrow {\frac{2}{3} \cdot 10;\frac{2}{3} \cdot 9} ) = (\overrightarrow {\frac{{20}}{3};6} ).$

$4)5\overrightarrow a + 9\overrightarrow b = 5 \cdot \overrightarrow {(2; - 7)} + 9 \cdot \overrightarrow {( - 5;0)} =$

обычно умножение координат на число выполняют устно:

$= \overrightarrow {(10; - 35)} + \overrightarrow {( - 45;0)} =$

применяем правило сложения векторов

$= \overrightarrow {(10 + ( - 45); - 35 + 0)} = \overrightarrow {( - 35; - 35)} .$

$5)6\overrightarrow b - 8\overrightarrow c = 6 \cdot \overrightarrow {( - 5;0)} - 8 \cdot \overrightarrow {(10;9)} = \overrightarrow {( - 30;0)} - \overrightarrow {(80;72)} =$