Как найти углы параллелограмма, если известен угол между высотой и биссектрисой угла параллелограмма?
Задача 1
Угол между биссектрисой тупого угла параллелограмма и высотой, проведенной из той же вершины, равен α. Найти углы параллелограмма.
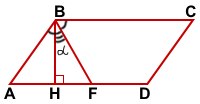Дано: ABCD — параллелограмм,
BH — высота, BF — биссектриса ∠ABC, ∠HBF=α
Найти: ∠A, ∠ABC, ∠C, ∠D
Решение:
Так как BH — высота параллелограмма, BH⊥BC, ∠HBC=90°.
Отсюда ∠FBC=∠HBC-∠HBF=90°-α.
Так как BF биссектриса — ∠ABC, ∠ABF=∠FBC=90°-α,
∠ABC=2·(90°-α)=180°-2α.
∠A+∠ABC=180° (как сумма внутренних односторонних углов при AD∥BC и секущей AB).
Следовательно, ∠A=180°-∠ABC=180°-(180°-2α)=2α.
Так как противолежащие углы параллелограмма равны, то
∠C=∠A=2α,
∠D=∠ABC=180°-2α.
Ответ: 2α, 2α,180°-2α, 180°-2α.
Задача 2
Угол между биссектрисой острого угла параллелограмма и высотой, проведенной из той же вершины, равен α. Найти углы параллелограмма.
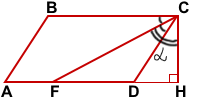Дано:ABCD — параллелограмм,
CH — высота, CF биссектриса — ∠BCD, ∠FCH=α
Найти: ∠A, ∠B, ∠BCD, ∠ADC
Решение:
Так как CH — высота параллелограмма, CH⊥BC, ∠BCH=90°.
Отсюда ∠BCF=∠BCH-∠FCH=90°-α.
Поскольку СF биссектриса — ∠BCD, ∠FCD=∠BCF=90°-α,
∠BCD=2·(90°-α)=180°-2α.
∠ADC+∠BCD=180° (как сумма внутренних односторонних углов при AD∥BC и секущей CD).
Следовательно, ∠ADC=180°-∠BCD=180°-(180°-2α)=2α.
∠A=∠BCD=180°-2α, ∠B=∠ADC=2α (как противолежащие углы параллелограмма).
Ответ: 2α, 2α,180°-2α, 180°-2α.
Таким образом, величины двух углов параллелограмма в два раза больше угла между биссектрисой и высотой, двух других — равны разности 180° и удвоенного угла между биссектрисой и высотой.