Угол между секущими

Утверждение

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.

ugol-mezhdu-sekushchimi

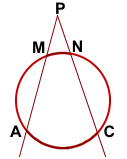
Доказать:

$\angle APC = \frac{1}{2}( \cup AC - \cup MN)$

Доказательство:

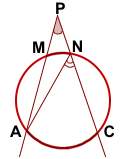ugol-mezhdu-sekushchimi-raven Проведём хорду AN.

Для треугольника APN ∠ANC — внешний угол при вершине N.

Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним,

∠ANC=∠APN+∠PAN,

∠APN=∠ANC-∠PAN.

∠ANC — вписанный угол, опирающийся на дугу AC,

∠PAN — вписанный угол, опирающийся на дугу MN.

Так как вписанный угол равен половине дуги, на которую он опирается, то

$\angle ANC = \frac{1}{2} \cup AC,$

$\angle PAN = \frac{1}{2} \cup MN,$

$\angle APC = \frac{1}{2} \cup AC - \frac{1}{2} \cup MN.$

Выносим за скобки общий множитель:

$\angle APC = \frac{1}{2}( \cup AC - \cup MN).$

Что и требовалось доказать.