Синус 135 |

Синус 135 градусов найдем по формуле приведения для синуса тупого угла от 90 до 180 градусов.

Утверждение:

$\sin {135^o} = \frac{{\sqrt 2 }}{2}$

Доказательство:

sinus 135

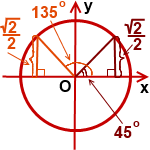
Синус угла альфа на единичной окружности — это ордината точки, полученной из точки (1;0) при повороте на угол альфа вокруг точки O.

Для синуса тупого угла (от 90º до 180º) имеет место следующая формула приведения:

$\sin ({180^0} - \alpha ) = \sin \alpha .$

Так как

${135^o} = {180^0} - {45^o},$

то воспользовавшись этой формулой приведения и значением синуса 45º, получаем:

$\sin {135^o} = \sin ({180^0} - {45^o}) = \sin {45^o} = \frac{{\sqrt 2 }}{2}.$

Что и требовалось доказать.

Если перевести 135 градусов в радианы:

${135^o} = \frac{{3\pi }}{4},$

то получим значение синуса 3П/4:

$\sin \frac{{3\pi }}{4} = \frac{{\sqrt 2 }}{2}.$

Синус 135 градусов